See part (1) and part (2) of this post here and here, respectively.
In part (2) of this post, we defined the lower central series of a group  and proved that
and proved that  is nilpotent if and only if
is nilpotent if and only if  for some
for some  We are now going to use this result to prove some facts about nilpotent groups.
We are now going to use this result to prove some facts about nilpotent groups.
Fact 1. Every subgroup of a nilpotent group is nilpotent.
Proof. Let  be a nilpotent group, and let
be a nilpotent group, and let  be a subgroup of
be a subgroup of 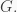 We first prove that
We first prove that  for all
for all  The proof is by induction. That is clear for
The proof is by induction. That is clear for 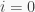 because
because  If the inclusion holds for
If the inclusion holds for 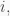 then
then
![\gamma_{i+1}(H)=[\gamma_i(H), H] \subseteq [\gamma_i(G),G]=\gamma_{i+1}(G),](https://s0.wp.com/latex.php?latex=%5Cgamma_%7Bi%2B1%7D%28H%29%3D%5B%5Cgamma_i%28H%29%2C+H%5D+%5Csubseteq+%5B%5Cgamma_i%28G%29%2CG%5D%3D%5Cgamma_%7Bi%2B1%7D%28G%29%2C&bg=f9f9f9&fg=333333&s=0&c=20201002)
which completes the induction. Now, since  is nilpotent,
is nilpotent,  for some integer
for some integer  Thus
Thus 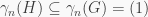 and so
and so  implying that
implying that  is nilpotent.
is nilpotent. 
Fact 2. Let  be a group, and let
be a group, and let  be a normal subgroup of
be a normal subgroup of 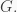
i) If 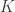 is a group, and
is a group, and  is a group homomorphism, then
is a group homomorphism, then  for all
for all 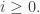
ii) If  is nilpotent, then
is nilpotent, then 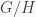 is nilpotent.
is nilpotent.
Proof. i) The proof is by induction. We have  and so the equality holds for
and so the equality holds for 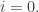 Now, if the equality holds for
Now, if the equality holds for 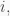 then
then
![\gamma_{i+1}(f(G))=[\gamma_i(f(G)),f(G)]=[f(\gamma_i(G)), f(G)]=f([\gamma_i(G),G])=f(\gamma_{i+1}(G)),](https://s0.wp.com/latex.php?latex=%5Cgamma_%7Bi%2B1%7D%28f%28G%29%29%3D%5B%5Cgamma_i%28f%28G%29%29%2Cf%28G%29%5D%3D%5Bf%28%5Cgamma_i%28G%29%29%2C+f%28G%29%5D%3Df%28%5B%5Cgamma_i%28G%29%2CG%5D%29%3Df%28%5Cgamma_%7Bi%2B1%7D%28G%29%29%2C&bg=f9f9f9&fg=333333&s=0&c=20201002)
which completes the induction.
ii) Let  be the natural group homomorphism. Since
be the natural group homomorphism. Since  is nilpotent,
is nilpotent,  for some integer
for some integer  and so, by i),
and so, by i),  implying that
implying that 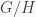 is nilpotent.
is nilpotent. 
Remark 1. Let  be a group with a normal subgroup
be a group with a normal subgroup  In Theorem 1, ii), in this post, we showed that
In Theorem 1, ii), in this post, we showed that  is solvable if and only if both
is solvable if and only if both 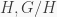 are solvable. In Remark 1 in the first part of this post, we showed that every nilpotent group is solvable. However, it is not true that if both
are solvable. In Remark 1 in the first part of this post, we showed that every nilpotent group is solvable. However, it is not true that if both 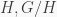 are nilpotent, then
are nilpotent, then  is nilpotent too. For example, the symmetric group
is nilpotent too. For example, the symmetric group 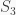 is not nilpotent, by Example 3 in the first part of this post, but both
is not nilpotent, by Example 3 in the first part of this post, but both  are nilpotent because they are abelian. However, if
are nilpotent because they are abelian. However, if  is in the center of
is in the center of  and
and 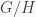 is nilpotent, then, as the next fact shows,
is nilpotent, then, as the next fact shows,  is nilpotent too.
is nilpotent too.
Fact 3. Let  be a group with the center
be a group with the center 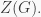
i) If 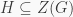 is a subgroup of
is a subgroup of  and
and 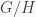 is nilpotent, then
is nilpotent, then  is nilpotent.
is nilpotent.
ii)  if and only if
if and only if 
Proof. i) Note that  is normal in
is normal in  because
because  Now, let
Now, let  be the natural group homomorphism. Since
be the natural group homomorphism. Since 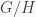 is nilpotent,
is nilpotent, 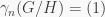 for some integer
for some integer  But, as we showed in the proof of Fact 2,
But, as we showed in the proof of Fact 2,  and so
and so 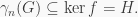 Thus
Thus
![\gamma_{n+1}(G)=[\gamma_n(G),G] \subseteq [H,G]=(1),](https://s0.wp.com/latex.php?latex=%5Cgamma_%7Bn%2B1%7D%28G%29%3D%5B%5Cgamma_n%28G%29%2CG%5D+%5Csubseteq+%5BH%2CG%5D%3D%281%29%2C&bg=f9f9f9&fg=333333&s=0&c=20201002)
because 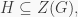 and so
and so 
ii) We showed in i) that if  then
then  Suppose now that
Suppose now that  Then
Then ![[\gamma_n(G),G]=\gamma_{n+1}(G)=(1)](https://s0.wp.com/latex.php?latex=%5B%5Cgamma_n%28G%29%2CG%5D%3D%5Cgamma_%7Bn%2B1%7D%28G%29%3D%281%29&bg=f9f9f9&fg=333333&s=0&c=20201002) and so
and so  Hence, if
Hence, if  is the natural group homomorphism, then, by Fact 2, i),
is the natural group homomorphism, then, by Fact 2, i),

and so 
Remark 2. In part (2) of this post, we defined the nilpotency class of a nilpotent group  as the smallest integer
as the smallest integer 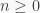 such that
such that  So, by Fact 3, ii),
So, by Fact 3, ii), 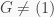 is a nilpotent group of class
is a nilpotent group of class  if and only if
if and only if  is a nilpotent group of class
is a nilpotent group of class  As the next Fact shows, this result may be used to prove nilpotency certain groups are nilpotent.
As the next Fact shows, this result may be used to prove nilpotency certain groups are nilpotent.
Fact 4. Let  be groups and let
be groups and let 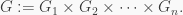 Then
Then  is nilpotent if and only if each
is nilpotent if and only if each  is nilpotent.
is nilpotent.
Proof. By induction over 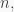 we only to prove the result for
we only to prove the result for  Suppose first that
Suppose first that  is nilpotent, and let
is nilpotent, and let 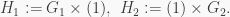 Then
Then  are normal subgroups of
are normal subgroups of  and we have the group isomorphisms
and we have the group isomorphisms 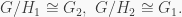 Thus, by Fact 2, ii), both
Thus, by Fact 2, ii), both  are nilpotent.
are nilpotent.
Conversely, suppose that  are nilpotent of class
are nilpotent of class  respectively, and let
respectively, and let  We prove, by induction over
We prove, by induction over 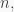 that
that  is nilpotent of class
is nilpotent of class 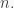 It is clear for
It is clear for 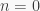 because then
because then  and so
and so  Also, if
Also, if  then both
then both  are abelian and at least one of them is non-trivial. Thus
are abelian and at least one of them is non-trivial. Thus  is a non-trivial abelian group hence nilpotent of class
is a non-trivial abelian group hence nilpotent of class  Suppose now that
Suppose now that  and consider the natural group homomorphism
and consider the natural group homomorphism

Clearly 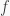 is onto and
is onto and  Thus
Thus  By Remark 2,
By Remark 2,  are nilpotent of class
are nilpotent of class  respectively. So, by induction,
respectively. So, by induction,  is nilpotent of class
is nilpotent of class  and hence, by Remark 2,
and hence, by Remark 2,  is nilpotent of class
is nilpotent of class 
Fact 5 (The Normalizer Condition). Let 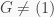 be a nilpotent group, and let
be a nilpotent group, and let  be a subgroup of
be a subgroup of 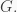 If
If  then
then 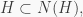 where
where 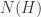 is the normalizer of
is the normalizer of  in
in 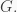
Proof. Suppose, to the contrary, that  Since
Since  is nilpotent,
is nilpotent,  for some integer
for some integer 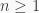 (note that we can’t have
(note that we can’t have 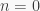 because
because  is non-trivial). Thus
is non-trivial). Thus  We also have that
We also have that  So there exists an integer
So there exists an integer 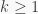 which is minimal with respect to this property that
which is minimal with respect to this property that  Hence
Hence
![[\gamma_{k-1}(G),H] \subseteq [\gamma_{k-1}(G),G]=\gamma_k(G) \subseteq H,](https://s0.wp.com/latex.php?latex=%5B%5Cgamma_%7Bk-1%7D%28G%29%2CH%5D+%5Csubseteq+%5B%5Cgamma_%7Bk-1%7D%28G%29%2CG%5D%3D%5Cgamma_k%28G%29+%5Csubseteq+H%2C&bg=f9f9f9&fg=333333&s=0&c=20201002)
and so  contradicting minimality of
contradicting minimality of 
See part (4) of this post here.
we say that a group
is
-abelian if
for all
Here we showed that if
where
is the center of
is abelian and if
is odd, then
is
-abelian. We now prove a much more interesting result.
be a group with the center
If
then
is
-aberlian.
be a transversal of
in
as defined in this post. Let
and let
be such that
Then
be any cycle in the decomposition of
into disjoint cycles. Then, by
we get that
is the product of
disjoint cycles, then we will have
identities of the form
Multiplying all the
identities together gives
On the other hand, by the Theorem in the post linked at the beginning of the proof, the map
defined by
is a group homomorphism. Hence
is a group homomorphism and so, for all
is
-abelian.
the proof was added by me.