Rings in this post may or may not have identity. As always, the ring of  matrices with entries from a ring
matrices with entries from a ring  is denoted by
is denoted by 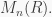
PI rings are arguably the most important generalization of commutative rings. This post is the first part of a series of posts about this fascinating class of rings.
Let 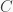 be a commutative ring with identity, and let
be a commutative ring with identity, and let 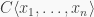 be the ring of polynomials in noncommuting indeterminates
be the ring of polynomials in noncommuting indeterminates 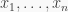 and with coefficients in
and with coefficients in 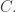 We will assume that each
We will assume that each 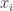 commutes with every element of
commutes with every element of 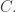 If
If  then
then 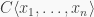 is just the ordinary commutative polynomial ring
is just the ordinary commutative polynomial ring ![C[x].](https://s0.wp.com/latex.php?latex=C%5Bx%5D.&bg=f9f9f9&fg=333333&s=0&c=20201002)
A monomial is an element of 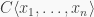 which is of the form
which is of the form 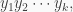 where
where 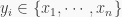 for all
for all  The degree of a monomial
The degree of a monomial 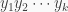 is defined to be
is defined to be  For example,
For example, 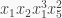 is a monomial of degree
is a monomial of degree 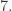 So an element of
So an element of 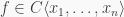 is a
is a 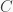 -linear combination of monomials, and we say that
-linear combination of monomials, and we say that 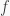 is monic if the coefficient of at least one of the monomials of the highest degree in
is monic if the coefficient of at least one of the monomials of the highest degree in 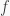 is
is  For example,
For example,  is not monic because none of the monomials of the highest degree, i.e.
is not monic because none of the monomials of the highest degree, i.e. 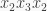 and
and 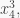 have coefficient
have coefficient 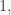 but
but 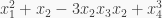 is monic.
is monic.
Definition 1. A ring  is called a polynomial identity ring, or PI ring for short, if there exists a positive integer
is called a polynomial identity ring, or PI ring for short, if there exists a positive integer  and a monic polynomial
and a monic polynomial 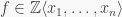 such that
such that  for all
for all 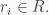 We then say that
We then say that  satisfies
satisfies 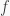 or
or 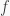 is an identity of
is an identity of 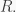
Definition 2. Let 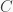 be a commutative ring with identity, and let
be a commutative ring with identity, and let  be a
be a 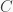 -algebra. If, in Definition 1, we replace
-algebra. If, in Definition 1, we replace  with
with 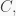 we will get the definition of a PI algebra. So
we will get the definition of a PI algebra. So  is called a PI algebra if there exists a positive integer
is called a PI algebra if there exists a positive integer  and a monic polynomial
and a monic polynomial 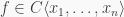 such that
such that  for all
for all 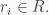 Note that since every ring is a
Note that since every ring is a  -algebra, every PI ring is a PI algebra.
-algebra, every PI ring is a PI algebra.
Example 1. Every commutative ring  is a PI ring.
is a PI ring.
Proof. Since  is commutative,
is commutative, 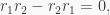 for all
for all 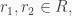 and therefore
and therefore  satisfies the monic polynomial
satisfies the monic polynomial 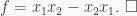
Remark 1. A PI ring could satisfy many polynomials. For example a finite field of order  satisfies the polynomial in Example 1, because it is commutative, and it also satisfies the polynomial
satisfies the polynomial in Example 1, because it is commutative, and it also satisfies the polynomial 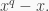 Another example is Boolean rings; they satisfy the polynomial in Example 1, because they are commutative, and they also satisfy the polynomial
Another example is Boolean rings; they satisfy the polynomial in Example 1, because they are commutative, and they also satisfy the polynomial 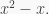
Example 2. If 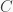 is a commutative ring with identity, then
is a commutative ring with identity, then 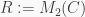 is a PI ring.
is a PI ring.
Proof. Let 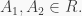 Then
Then 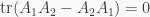 and so, by Cayley-Hamilton,
and so, by Cayley-Hamilton,
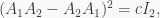
for some  Thus
Thus 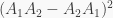 commutes with every element of
commutes with every element of  i.e.,
i.e.,
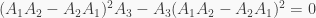
for all 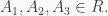 Thus
Thus  satisfies the monic polynomial
satisfies the monic polynomial
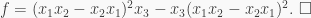
Example 3. The division ring of real quaternions 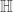 is a PI ring.
is a PI ring.
Proof. Recall that 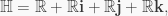 where
where 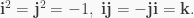 Let
Let

It is easy to see that 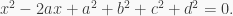 Thus, since
Thus, since  are in the center of
are in the center of  we get that
we get that 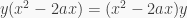 for all
for all  So
So 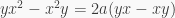 and hence, since
and hence, since  is central,
is central, 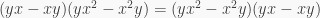 for all
for all 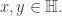 Therefore
Therefore 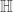 satisfies the monic polynomial
satisfies the monic polynomial 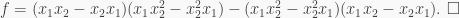
Remark 2. If  is a PI ring with identity, then
is a PI ring with identity, then  could satisfy a polynomial with a nonzero constant. For example, the ring
could satisfy a polynomial with a nonzero constant. For example, the ring 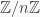 satisfies the polynomial in Example 1, and it also satisfies the polynomial
satisfies the polynomial in Example 1, and it also satisfies the polynomial 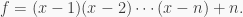 Now suppose that
Now suppose that  has no identity, and
has no identity, and 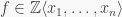 has a nonzero constant
has a nonzero constant 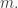 So
So 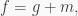 where
where 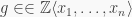 has a zero constant. Now, what is
has a zero constant. Now, what is 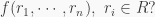 Well, It is not defined because it is supposed to be
Well, It is not defined because it is supposed to be 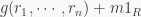 but
but 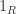 does not exist. So if
does not exist. So if  has no identity, all identities of
has no identity, all identities of  must have zero constants.
must have zero constants.
Example 4. Any subring or homomorphic image of a PI ring is a PI ring.
Proof. If  satisfies
satisfies 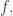 then obviously any subring of
then obviously any subring of  satisfies
satisfies 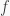 too. If
too. If  is a homomorphic image of
is a homomorphic image of  then
then 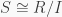 for some ideal
for some ideal 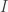 of
of 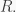 Now, it is clear that for any
Now, it is clear that for any 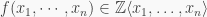 and any
and any 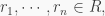 we have
we have 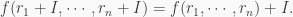 Hence if
Hence if  satisfies
satisfies 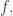 then
then 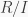 satisfies
satisfies 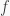 too.
too. 
Example 5. If 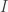 is a nilpotent ideal of a ring
is a nilpotent ideal of a ring  and
and 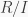 is a PI ring, then
is a PI ring, then  is a PI ring.
is a PI ring.
Proof. So 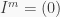 for some positive integer
for some positive integer 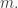 Now suppose that
Now suppose that 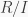 satisfies a monic polynomial
satisfies a monic polynomial 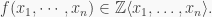 Then
Then
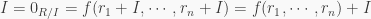
for all 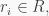 and so
and so 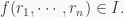 Thus
Thus 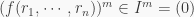 and hence
and hence  satisfies the monic polynomial
satisfies the monic polynomial 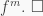
Example 6. A finite direct product of PI rings is a PI ring.
Proof. By induction, we only need to prove that for a direct product two PI rings. So let 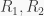 be PI rings that, respectively, satisfy
be PI rings that, respectively, satisfy 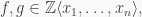 and let
and let 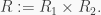 It is clear that for any polynomial
It is clear that for any polynomial  and
and 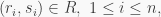 we have
we have

Therefore
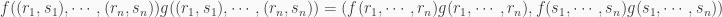
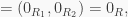
because 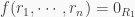 and
and 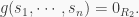 So
So  satisfies the monic polynomial
satisfies the monic polynomial 
Exercise. Let  be a ring with the center
be a ring with the center 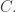 Suppose that for every
Suppose that for every 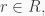 there exist
there exist 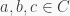 such that
such that 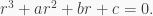 Show that
Show that  is a PI ring.
is a PI ring.
Hint. See the proof of Example 3.
Note. The reference for this post is Section 1, Chapter 13 of the book Noncommutative Noetherian Rings by McConnell and Robson. Example 3 was added by me.
we say that a group
is
-abelian if
for all
Here we showed that if
where
is the center of
is abelian and if
is odd, then
is
-abelian. We now prove a much more interesting result.
be a group with the center
If
then
is
-aberlian.
be a transversal of
in
as defined in this post. Let
and let
be such that
Then
be any cycle in the decomposition of
into disjoint cycles. Then, by
we get that
is the product of
disjoint cycles, then we will have
identities of the form
Multiplying all the
identities together gives
On the other hand, by the Theorem in the post linked at the beginning of the proof, the map
defined by
is a group homomorphism. Hence
is a group homomorphism and so, for all
is
-abelian.
the proof was added by me.